Home  ›  Algebra 2 Review Guide 6a Part 2 Solve Each System by Elimination

Algebra 2 Review Guide 6a Part 2 Solve Each System by Elimination

Written By Monday, April 18, 2022 Add Comment Edit

Systems of Linear Equations

42 Solve Systems of Equations past Elimination

Learning Objectives

By the end of this section, you will be able to:

  • Solve a system of equations past elimination
  • Solve applications of systems of equations by elimination
  • Choose the most convenient method to solve a system of linear equations

Before you get started, take this readiness quiz.

  1. Simplify -5\left(6-3a\right).
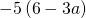    If you missed this trouble, review (Figure).
  2. Solve the equation \frac{1}{3}x+\frac{5}{8}=\frac{31}{24}.
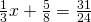    If y'all missed this problem, review (Figure).

Nosotros accept solved systems of linear equations past graphing and past substitution. Graphing works well when the variable coefficients are modest and the solution has integer values. Substitution works well when we can easily solve one equation for 1 of the variables and not have too many fractions in the resulting expression.

The tertiary method of solving systems of linear equations is called the Elimination Method. When we solved a organisation by substitution, we started with ii equations and two variables and reduced it to 1 equation with one variable. This is what nosotros'll do with the elimination method, too, simply we'll accept a unlike way to get there.

Solve a System of Equations by Elimination

The Elimination Method is based on the Addition Holding of Equality. The Improver Property of Equality says that when you add the aforementioned quantity to both sides of an equation, you still accept equality. We will extend the Addition Holding of Equality to say that when you add equal quantities to both sides of an equation, the results are equal.

For whatever expressions a, b, c, and d,

\begin{array}{cccc}\text{if}\hfill & \hfill a& =\hfill & b\hfill \\ \text{and}\hfill & \hfill c& =\hfill & d\hfill \\ \text{then}\hfill & \hfill a+c& =\hfill & b+d\hfill \end{array}

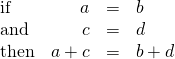
To solve a system of equations past elimination, we start with both equations in standard form. So we decide which variable will be easiest to eliminate. How do nosotros determine? We want to take the coefficients of one variable be opposites, and then that we tin add together the equations together and eliminate that variable.

Notice how that works when nosotros add together these ii equations together:

\begin{array}{c}3x+y=5\hfill \\ \underset{\text{_________}}{2x-y=0}\hfill \\ 5x\phantom{\rule{1.7em}{0ex}}=5\hfill \end{array}

The y's add together to zero and we have ane equation with one variable.

Let's try some other one:

\left\{\begin{array}{c}x+4y=2\hfill \\ 2x+5y=-2\hfill \end{array}

This time nosotros don't meet a variable that can be immediately eliminated if we add the equations.

But if we multiply the showtime equation past −2, nosotros volition make the coefficients of x opposites. Nosotros must multiply every term on both sides of the equation by −2.

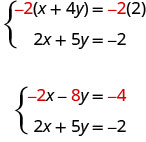
This figure shows two equations. The first is negative 2 times x plus 4y in parentheses equals negative 2 times 2. The second is 2x + 5y = negative 2. This figure shows two equations. The first is negative 2x minus 8y = negative 4. The second is 2x + 5y = -negative 2.

Now nosotros see that the coefficients of the x terms are opposites, then 10 will be eliminated when we add together these 2 equations.

Add the equations yourself—the event should be −iiiy = −six. And that looks piece of cake to solve, doesn't it? Here is what it would look like.

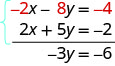
This figure shows two equations being added together. The first is negative 2x – 8y = −4 and 2x plus 5y = negative 2. The answer is negative 3y = negative 6.

We'll do one more:

\left\{\begin{array}{c}4x-3y=10\hfill \\ 3x+5y=-7\hfill \end{array}

Information technology doesn't announced that nosotros tin can get the coefficients of i variable to be opposites by multiplying ane of the equations past a constant, unless we utilise fractions. So instead, nosotros'll have to multiply both equations past a abiding.

We can make the coefficients of 10 be opposites if we multiply the showtime equation by 3 and the 2nd by −4, so nosotros become 12x and −12x.

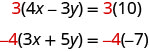
This figure shows two equations. The first is 3 times 4x minus 3y in parentheses equals 3 times 10. The second is negative 4 times 3x plus 5y in parentheses equals negative 4 times negative 7.

This gives us these two new equations:

\left\{\begin{array}{c}\phantom{\rule{1.1em}{0ex}}12x-9y=30\hfill \\ -12x-20y=28\hfill \end{array}

When we add these equations,

\begin{array}{c}\left\{\begin{array}{c}\phantom{\rule{1.1em}{0ex}}12x-9y=30\hfill \\ \underset{\text{_____________}}{-12x-20y=28}\hfill \end{array}\\ \hfill -29y=58\end{array}

the ten's are eliminated and we simply have −29y = 58.

Once we get an equation with just one variable, nosotros solve it. And then nosotros substitute that value into 1 of the original equations to solve for the remaining variable. And, equally e'er, we check our answer to brand sure it is a solution to both of the original equations.

Now nosotros'll see how to apply elimination to solve the same organisation of equations we solved by graphing and by substitution.

How to Solve a System of Equations by Emptying

Solve the system by elimination. \left\{\begin{array}{c}2x+y=7\hfill \\ x-2y=6\hfill \end{array}

Solve the system by emptying. \left\{\begin{array}{c}3x+y=5\hfill \\ 2x-3y=7\hfill \end{array}

\left(2,-1\right)

Solve the system by elimination. \left\{\begin{array}{c}4x+y=-5\hfill \\ -2x-2y=-2\hfill \end{array}

\left(-2,3\right)

The steps are listed below for piece of cake reference.

How to solve a system of equations past elimination.

  1. Write both equations in standard class. If any coefficients are fractions, clear them.
  2. Make the coefficients of one variable opposites.
    • Determine which variable you will eliminate.
    • Multiply one or both equations so that the coefficients of that variable are opposites.
  3. Add the equations resulting from Step two to eliminate 1 variable.
  4. Solve for the remaining variable.
  5. Substitute the solution from Footstep four into i of the original equations. Then solve for the other variable.
  6. Write the solution as an ordered pair.
  7. Bank check that the ordered pair is a solution to both original equations.

First we'll do an example where we can eliminate one variable correct away.

Solve the system by emptying. \left\{\begin{array}{c}x+y=10\hfill \\ x-y=12\hfill \end{array}

Solve the arrangement by elimination. \left\{\begin{array}{c}2x+y=5\hfill \\ x-y=4\hfill \end{array}

\left(3,-1\right)

Solve the system by elimination. \left\{\begin{array}{c}x+y=3\hfill \\ -2x-y=-1\hfill \end{array}

\left(-2,5\right)

In (Figure), we volition be able to make the coefficients of ane variable opposites by multiplying one equation by a abiding.

Solve the system by elimination. \left\{\begin{array}{c}3x-2y=-2\hfill \\ 5x-6y=10\hfill \end{array}

Solve the system past elimination. \left\{\begin{array}{c}4x-3y=1\hfill \\ 5x-9y=-4\hfill \end{array}

\left(1,1\right)

Solve the system by emptying. \left\{\begin{array}{c}3x+2y=2\hfill \\ 6x+5y=8\hfill \end{array}

\left(-2,4\right)

At present we'll do an instance where nosotros need to multiply both equations by constants in order to make the coefficients of one variable opposites.

Solve the system by elimination. \left\{\begin{array}{c}4x-3y=9\hfill \\ 7x+2y=-6\hfill \end{array}

Solve the system past elimination. \left\{\begin{array}{c}3x-4y=-9\hfill \\ 5x+3y=14\hfill \end{array}

\left(1,3\right)

Solve the system by elimination. \left\{\begin{array}{c}7x+8y=4\hfill \\ 3x-5y=27\hfill \end{array}

\left(4,-3\right)

When the organisation of equations contains fractions, we volition first clear the fractions by multiplying each equation past its LCD.

Solve the system by elimination. \left\{\begin{array}{c}x+\frac{1}{2}y=6\hfill \\ \frac{3}{2}x+\frac{2}{3}y=\frac{17}{2}\hfill \end{array}

Solve the system past elimination. \left\{\begin{array}{c}\frac{1}{3}x-\frac{1}{2}y=1\hfill \\ \frac{3}{4}x-y=\frac{5}{2}\hfill \end{array}

\left(6,2\right)

Solve the system by elimination. \left\{\begin{array}{c}x+\frac{3}{5}y=-\frac{1}{5}\hfill \\ -\frac{1}{2}x-\frac{2}{3}y=\frac{5}{6}\hfill \end{array}

\left(1,-2\right)

In the Solving Systems of Equations by Graphing nosotros saw that not all systems of linear equations have a single ordered pair equally a solution. When the 2 equations were really the aforementioned line, there were infinitely many solutions. We called that a consistent system. When the two equations described parallel lines, there was no solution. We called that an inconsistent organisation.

Solve the arrangement by elimination. \left\{\begin{array}{c}3x+4y=12\hfill \\ y=3-\frac{3}{4}x\hfill \end{array}

Solution

\left\{\begin{array}{c}3x+4y=12\hfill \\ y=3-\frac{3}{4}x\hfill \end{array}
Write the second equation in standard course. \left\{\begin{array}{ccc}\hfill 3x+4y& =\hfill & 12\hfill \\ \hfill \frac{3}{4}x+y& =\hfill & 3\hfill \end{array}
Clear the fractions by multiplying the 2d equation past 4. \left\{\begin{array}{ccc}\hfill 3x+4y& =\hfill & 12\hfill \\ \hfill 4\left(\frac{3}{4}x+y\right)& =\hfill & 4\left(3\right)\hfill \end{array}
Simplify. \left\{\begin{array}{ccc}\hfill 3x+4y& =\hfill & 12\hfill \\ \hfill 3x+4y& =\hfill & 12\hfill \end{array}
To eliminate a variable, nosotros multiply the 2nd equation by -1.
Simplify and add.		 \begin{array}{c}\phantom{\rule{0.2em}{0ex}}\underset{\text{________________}}{\left\{\begin{array}{ccc}\hfill 3x+4y& =\hfill & 12\hfill \\ \hfill -3x-4y& =\hfill & -12\hfill \end{array}}\hfill \\ \hfill 0=0\hfill \end{array}

This is a true statement. The equations are consistent simply dependent. Their graphs would be the same line. The arrangement has infinitely many solutions.

Later on we cleared the fractions in the 2nd equation, did yous notice that the two equations were the aforementioned? That means we have coincident lines.

Solve the arrangement by elimination. \left\{\begin{array}{c}5x-3y=15\hfill \\ y=-5+\frac{5}{3}x\hfill \end{array}

infinitely many solutions

Solve the system past elimination. \left\{\begin{array}{c}x+2y=6\hfill \\ y=-\frac{1}{2}x+3\hfill \end{array}

infinitely many solutions

Solve the organisation by elimination. \left\{\begin{array}{c}-6x+15y=10\hfill \\ 2x-5y=-5\hfill \end{array}

Solution

The equations are in standard form. \left\{\begin{array}{ccc}\hfill -6x+15y& =\hfill & 10\hfill \\ \hfill 2x-5y& =\hfill & -5\hfill \end{array}
Multiply the second equation by iii to eliminate a variable. \left\{\begin{array}{ccc}\hfill -6x+15y& =\hfill & 10\hfill \\ \hfill 3\left(2x-5y\right)& =\hfill & 3\left(-5\right)\hfill \end{array}
Simplify and add. \begin{array}{c}\underset{\text{__________________}}{\left\{\begin{array}{ccc}\hfill -6x+15y& =\hfill & \phantom{\rule{0.5em}{0ex}}10\hfill \\ \hfill 6x-15y& =\hfill & -15\hfill \end{array}}\\ \hfill 0\ne -5\hfill \end{array}

This argument is false. The equations are inconsistent and then their graphs would be parallel lines.

The system does not accept a solution.

Solve the system by emptying. \left\{\begin{array}{c}-3x+2y=8\hfill \\ 9x-6y=13\hfill \end{array}

no solution

Solve the system by elimination. \left\{\begin{array}{c}7x-3y=-2\hfill \\ -14x+6y=8\hfill \end{array}

no solution

Solve Applications of Systems of Equations by Elimination

Some applications problems translate directly into equations in standard class, so we will use the elimination method to solve them. Equally earlier, we use our Problem Solving Strategy to help u.s.a. stay focused and organized.

The sum of two numbers is 39. Their difference is 9. Find the numbers.

The sum of two numbers is 42. Their difference is 8. Find the numbers.

The numbers are 25 and 17.

The sum of two numbers is −15. Their divergence is −35. Discover the numbers.

The numbers are −25 and ten.

Joe stops at a burger restaurant every day on his fashion to work. Mon he had one order of medium fries and two small sodas, which had a total of 620 calories. Tuesday he had two orders of medium fries and one small soda, for a full of 820 calories. How many calories are there in one lodge of medium fries? How many calories in one minor soda?

Malik stops at the grocery store to buy a handbag of diapers and 2 cans of formula. He spends a full of ?37. The next week he stops and buys two bags of diapers and five cans of formula for a total of ?87. How much does a bag of diapers cost? How much is one tin can of formula?

The bag of diapers costs ?11 and the can of formula costs ?xiii.

To get her daily intake of fruit for the day, Sasha eats a banana and 8 strawberries on Wednesday for a calorie count of 145. On the following Midweek, she eats two bananas and v strawberries for a total of 235 calories for the fruit. How many calories are there in a assistant? How many calories are in a strawberry?

There are 105 calories in a banana and five calories in a strawberry.

Choose the Most Convenient Method to Solve a System of Linear Equations

When you will have to solve a organisation of linear equations in a later math class, you lot will usually not be told which method to utilize. Yous will need to make that decision yourself. And then you'll desire to choose the method that is easiest to practise and minimizes your run a risk of making mistakes.

This table has two rows and three columns. The first row labels the columns as

For each system of linear equations decide whether it would be more convenient to solve it by substitution or emptying. Explicate your answer.

ⓐ \left\{\begin{array}{c}3x+8y=40\hfill \\ 7x-4y=-32\hfill \end{array} ⓑ \left\{\begin{array}{c}5x+6y=12\hfill \\ y=\frac{2}{3}x-1\hfill \end{array}

Solution

ⓐ \begin{array}{ccc}& & \left\{\begin{array}{c}3x+8y=40\hfill \\ 7x-4y=-32\hfill \end{array}\hfill \end{array}
Since both equations are in standard grade, using emptying will be most convenient.
ⓑ \begin{array}{ccc}& & \left\{\begin{array}{c}5x+6y=12\hfill \\ y=\frac{2}{3}x-1\hfill \end{array}\hfill \end{array}
Since one equation is already solved for y, using substitution volition exist almost convenient.

For each organization of linear equations, decide whether it would be more convenient to solve information technology by substitution or elimination. Explain your reply.

ⓐ \left\{\begin{array}{c}4x-5y=-32\hfill \\ 3x+2y=-1\hfill \end{array} ⓑ \left\{\begin{array}{c}x=2y-1\hfill \\ 3x-5y=-7\hfill \end{array}

ⓐ Since both equations are in standard form, using elimination volition exist virtually user-friendly. ⓑ Since one equation is already solved for x, using substitution will be about convenient.

For each arrangement of linear equations, decide whether it would exist more convenient to solve it by substitution or elimination. Explicate your reply.

ⓐ \left\{\begin{array}{c}y=2x-1\hfill \\ 3x-4y=-6\hfill \end{array} ⓑ \left\{\begin{array}{c}6x-2y=12\hfill \\ 3x+7y=-13\hfill \end{array}

ⓐ Since ane equation is already solved for y, using substitution will be most convenient; ⓑ Since both equations are in standard form, using elimination will be virtually convenient.

Central Concepts

  • To Solve a Organization of Equations by Elimination
    1. Write both equations in standard class. If any coefficients are fractions, clear them.
    2. Make the coefficients of i variable opposites.
      • Decide which variable you volition eliminate.
      • Multiply i or both equations so that the coefficients of that variable are opposites.
    3. Add the equations resulting from Stride ii to eliminate one variable.
    4. Solve for the remaining variable.
    5. Substitute the solution from Step 4 into 1 of the original equations. Then solve for the other variable.
    6. Write the solution as an ordered pair.
    7. Cheque that the ordered pair is a solution to both original equations.

Practice Makes Perfect

Solve a System of Equations by Emptying

In the following exercises, solve the systems of equations by elimination.

\left\{\begin{array}{c}5x+2y=2\hfill \\ -3x-y=0\hfill \end{array}

\left\{\begin{array}{c}-3x+y=-9\hfill \\ x-2y=-12\hfill \end{array}

(half dozen, 9)

\left\{\begin{array}{c}6x-5y=-1\hfill \\ 2x+y=13\hfill \end{array}

\left\{\begin{array}{c}3x-y=-7\hfill \\ 4x+2y=-6\hfill \end{array}

\left(-2,1\right)

\left\{\begin{array}{c}x+y=-1\hfill \\ x-y=-5\hfill \end{array}

\left\{\begin{array}{c}x+y=-8\hfill \\ x-y=-6\hfill \end{array}

\left(-7,-1\right)

\left\{\begin{array}{c}3x-2y=1\hfill \\ -x+2y=9\hfill \end{array}

\left\{\begin{array}{c}-7x+6y=-10\hfill \\ x-6y=22\hfill \end{array}

\left(-2,-4\right)

\left\{\begin{array}{c}3x+2y=-3\hfill \\ -x-2y=-19\hfill \end{array}

\left\{\begin{array}{c}5x+2y=1\hfill \\ -5x-4y=-7\hfill \end{array}

\left(-1,3\right)

\left\{\begin{array}{c}6x+4y=-4\hfill \\ -6x-5y=8\hfill \end{array}

\left\{\begin{array}{c}3x-4y=-11\hfill \\ x-2y=-5\hfill \end{array}

\left(-1,2\right)

\left\{\begin{array}{c}5x-7y=29\hfill \\ x+3y=-3\hfill \end{array}

\left\{\begin{array}{c}6x-5y=-75\hfill \\ -x-2y=-13\hfill \end{array}

\left(-5,9\right)

\left\{\begin{array}{c}-x+4y=8\hfill \\ 3x+5y=10\hfill \end{array}

\left\{\begin{array}{c}2x-5y=7\hfill \\ 3x-y=17\hfill \end{array}

(half dozen, 1)

\left\{\begin{array}{c}5x-3y=-1\hfill \\ 2x-y=2\hfill \end{array}

\left\{\begin{array}{c}7x+y=-4\hfill \\ 13x+3y=4\hfill \end{array}

\left(-2,10\right)

\left\{\begin{array}{c}-3x+5y=-13\hfill \\ 2x+y=-26\hfill \end{array}

\left\{\begin{array}{c}3x-5y=-9\hfill \\ 5x+2y=16\hfill \end{array}

(2, 3)

\left\{\begin{array}{c}4x-3y=3\hfill \\ 2x+5y=-31\hfill \end{array}

\left\{\begin{array}{c}4x+7y=14\hfill \\ -2x+3y=32\hfill \end{array}

\left(-7,6\right)

\left\{\begin{array}{c}5x+2y=21\hfill \\ 7x-4y=9\hfill \end{array}

\left\{\begin{array}{c}3x+8y=-3\hfill \\ 2x+5y=-3\hfill \end{array}

\left(-9,3\right)

\left\{\begin{array}{c}11x+9y=-5\hfill \\ 7x+5y=-1\hfill \end{array}

\left\{\begin{array}{c}3x+8y=67\hfill \\ 5x+3y=60\hfill \end{array}

(9, five)

\left\{\begin{array}{c}2x+9y=-4\hfill \\ 3x+13y=-7\hfill \end{array}

\left\{\begin{array}{c}\frac{1}{3}x-y=-3\hfill \\ x+\frac{5}{2}y=2\hfill \end{array}

\left(-3,2\right)

\left\{\begin{array}{c}x+\frac{1}{2}y=\frac{3}{2}\hfill \\ \frac{1}{5}x-\frac{1}{5}y=3\hfill \end{array}

\left\{\begin{array}{c}x+\frac{1}{3}y=-1\hfill \\ \frac{1}{2}x-\frac{1}{3}y=-2\hfill \end{array}

\left(-2,3\right)

\left\{\begin{array}{c}\frac{1}{3}x-y=-3\hfill \\ \frac{2}{3}x+\frac{5}{2}y=3\hfill \end{array}

\left\{\begin{array}{c}2x+y=3\hfill \\ 6x+3y=9\hfill \end{array}

infinitely many solutions

\left\{\begin{array}{c}x-4y=-1\hfill \\ -3x+12y=3\hfill \end{array}

\left\{\begin{array}{c}-3x-y=8\hfill \\ 6x+2y=-16\hfill \end{array}

infinitely many solutions

\left\{\begin{array}{c}4x+3y=2\hfill \\ 20x+15y=10\hfill \end{array}

\left\{\begin{array}{c}3x+2y=6\hfill \\ -6x-4y=-12\hfill \end{array}

infinitely many solutions

\left\{\begin{array}{c}5x-8y=12\hfill \\ 10x-16y=20\hfill \end{array}

\left\{\begin{array}{c}-11x+12y=60\hfill \\ -22x+24y=90\hfill \end{array}

inconsistent, no solution

\left\{\begin{array}{c}7x-9y=16\hfill \\ -21x+27y=-24\hfill \end{array}

\left\{\begin{array}{c}5x-3y=15\hfill \\ y=\frac{5}{3}x-2\hfill \end{array}

inconsistent, no solution

\left\{\begin{array}{c}2x+4y=7\hfill \\ y=-\frac{1}{2}x-4\hfill \end{array}

Solve Applications of Systems of Equations past Emptying

In the following exercises, interpret to a system of equations and solve.

The sum of two numbers is 65. Their difference is 25. Discover the numbers.

The numbers are 20 and 45.

The sum of two numbers is 37. Their departure is 9. Observe the numbers.

The sum of two numbers is −27. Their departure is −59. Find the numbers.

The numbers are 16 and −43.

The sum of two numbers is −45. Their deviation is −89. Find the numbers.

Andrea is buying some new shirts and sweaters. She is able to buy three shirts and 2 sweaters for ?114 or she is able to buy two shirts and iv sweaters for ?164. How much does a shirt price? How much does a sweater cost?

A shirt costs ?16 and a sweater costs ?33.

Peter is buying part supplies. He is able to purchase three packages of paper and four staplers for ?40 or he is able to buy 5 packages of newspaper and half dozen staplers for ?62. How much does a package of paper cost? How much does a stapler cost?

The full amount of sodium in 2 hot dogs and 3 cups of cottage cheese is 4720 mg. The total amount of sodium in 5 hot dogs and 2 cups of cottage cheese is 6300 mg. How much sodium is in a hot canis familiaris? How much sodium is in a cup of cottage cheese?

There are 860 mg in a hot domestic dog. There are 1,000 mg in a cup of cottage cheese.

The total number of calories in 2 hot dogs and iii cups of cottage cheese is 960 calories. The total number of calories in 5 hot dogs and 2 cups of cottage cheese is 1190 calories. How many calories are in a hot domestic dog? How many calories are in a cup of cottage cheese?

Choose the Most Convenient Method to Solve a System of Linear Equations

In the post-obit exercises, determine whether information technology would be more convenient to solve the organisation of equations past substitution or emptying.


 ⓐ \left\{\begin{array}{c}8x-15y=-32\hfill \\ 6x+3y=-5\hfill \end{array}
ⓑ \left\{\begin{array}{c}x=4y-3\hfill \\ 4x-2y=-6\hfill \end{array}

ⓐ elimination ⓑ substitution


 ⓐ \left\{\begin{array}{c}y=7x-5\hfill \\ 3x-2y=16\hfill \end{array}
ⓑ \left\{\begin{array}{c}12x-5y=-42\hfill \\ 3x+7y=-15\hfill \end{array}


ⓐ \left\{\begin{array}{c}y=4x+9\hfill \\ 5x-2y=-21\hfill \end{array}
ⓑ \left\{\begin{array}{c}9x-4y=24\hfill \\ 3x+5y=-14\hfill \end{array}

ⓐ substitution ⓑ elimination


 ⓐ \left\{\begin{array}{c}14x-15y=-30\hfill \\ 7x+2y=10\hfill \end{array}
ⓑ \left\{\begin{array}{c}x=9y-11\hfill \\ 2x-7y=-27\hfill \end{array}

Everyday Math

ⓐ r=4 ⓑ c=1

Writing Exercises

Solve the arrangement
\left\{\begin{array}{c}x+y=10\hfill \\ 5x+8y=56\hfill \end{array}

ⓐ by exchange
ⓑ by graphing
ⓒ Which method do you prefer? Why?

  1. ⓐ (8, 2)
  2. ⓑ
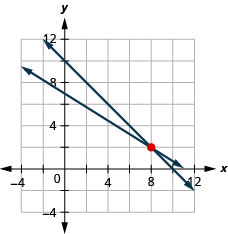
    This image is a graph that shows the solution to the system
  3. ⓒ Answers volition vary.

Solve the system
\left\{\begin{array}{c}x+y=-12\hfill \\ y=4-\frac{1}{2}x\hfill \end{array}

ⓐ by commutation
ⓑ by graphing
ⓒ Which method do yous adopt? Why?

Self Check

ⓐ Later on completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

This figure shows a table with four rows and four columns. The columns are labeled,

ⓑ What does this checklist tell yous well-nigh your mastery of this department? What steps will you take to improve?

vessgother.blogspot.com

Source: https://opentextbc.ca/elementaryalgebraopenstax/chapter/solve-systems-of-equations-by-elimination/

0 Response to "Algebra 2 Review Guide 6a Part 2 Solve Each System by Elimination"

Post a Comment

Subscribe to: Post Comments (Atom)

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel